GATE CSE 1991 | Question: 02-iv

Question

Match the pairs in the following questions by writing the corresponding letters only.
$$\begin{array}{|c|l|c|l|} \hline A. & \text{The number of distinct binary tree} & P. & \frac{n!}{2} \\& \text{ with n nodes.}\\ \hline B. &  \text{The number of binary strings of the length } & Q. & \binom{3n}{n} \\& \text{of 2n with an equal number of 0’s and 1’s}  \\ \hline C. & \text{The number of even permutation of n } & R. & \binom{2n}{n} \\& \text{ objects.}\\ \hline D. & \text {The number of binary strings of length 6n } & S. & \frac{1}{1+n}\binom{2n}{n} \\& \text{which are palindromes with 2n 0’s.} \\ \hline \end{array}$$

Comments

Lakshman Patel RJIT

Thank you for fixing this question

---

A --- S
B ---R
C ---P
D ---Q

In palindrome we select half rest all are same previous.

---

D))  first half = $3n$
number of $0$s in the first half =  $n$
number of $1$s the first half = $2n$
$\text{Total number of strings} = \binom{3n}{n} $

Answer 1

• A. $- S$  Catalan number https://gatecse.in/number-of-binary-trees-possible-with-n-nodes/
• B. $- R$  Choosing $n$ locations for $0$'s out of $2n$ locations. The remaining $n$ locations are filled with $1$'s (no selection required).
• C. $- P$  An even permutation is a permutation obtainable from an even number of two-element swaps, For a set of $n$ elements and $n>2$, there are $n!/2$ even permutations.
  Ref - http://mathworld.wolfram.com/EvenPermutation.html
• D.  $- Q$ 

Length $= 6n$, as it is palindrome, we need to select only the first half part of the string.

Total length to consider is $3n$ (Remaining $3n$ will be revese of this $3n$)

Now, choose $n \ 0's$ out of $3n$. So Q is correct for D.

Comments

nice explaination sir

---

refer here for even permutation def.

P.S. : Transpostion is nothing but swap, so basically even no. of swap

 

---

For option Q when we take half part of the string that's 3n we choose 2n positions for 0's according to the option == choosing n position for the 1's that's 3nC2n=3nCn.

Answer 2

Answer:

A - S
B - R
C - P
D - Q

Answer 3

It will be $\frac {n!}{2}$

using the property of symmetry.

http://mathworld.wolfram.com/EvenPermutation.html

Answer 4

An even permutation is a permutation obtainable from an even number of two-element swaps, For initial set 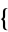1,2,3,4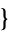, the twelve even permutations are those with zero swaps: (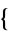1,2,3,4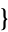); and those with two swaps: (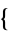1,3,4,2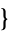, 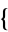1,4,2,3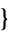, 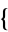2,1,4,3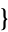, 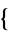2,3,1,4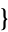, 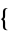2,4,3,1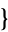, 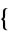3,1,2,4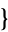, 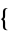3,2,4,1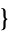, 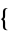3,4,1,2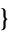, 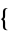4,1,3,2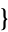, 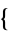4,2,1,3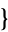, 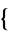4,3,2,1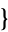). etc.

For a set of  n elements and n>2, there are n! / 2 even permutations, which is the same as the number of odd permutations